(Blog post written by Xiao Zhang)
Motivated by the empirical hardness of developing robust classifiers against adversarial perturbations, researchers began asking the question “Does there even exist a robust classifier?”. This is formulated as the intrinsic robustness problem (Mahloujifar et al., 2019), where the goal is to characterize the maximum adversarial robustness possible for a given robust classification problem. Building upon the connection between adversarial robustness and classifier’s error region, it has been shown that if we restrict the search to the set of imperfect classifiers, the intrinsic robustness problem can be reduced to the concentration of measure problem.
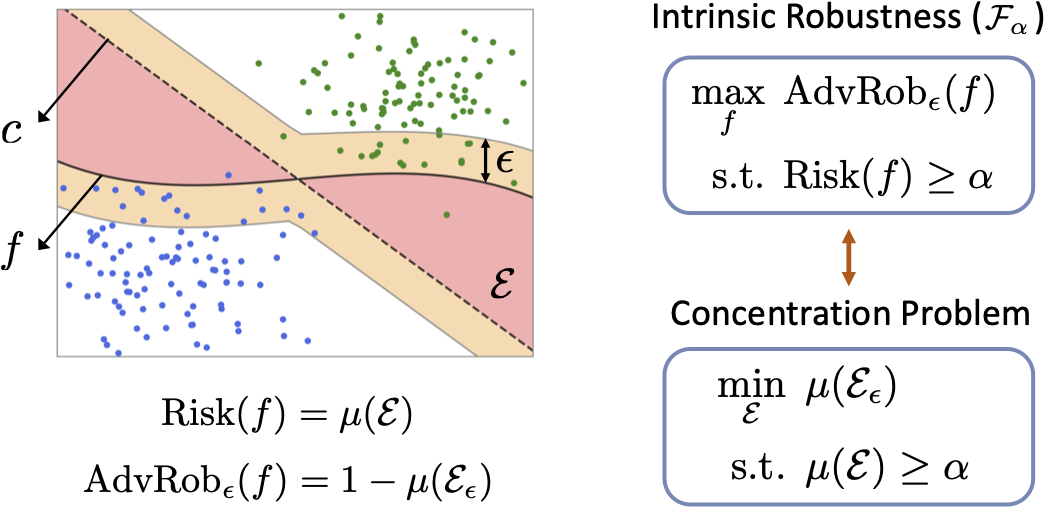
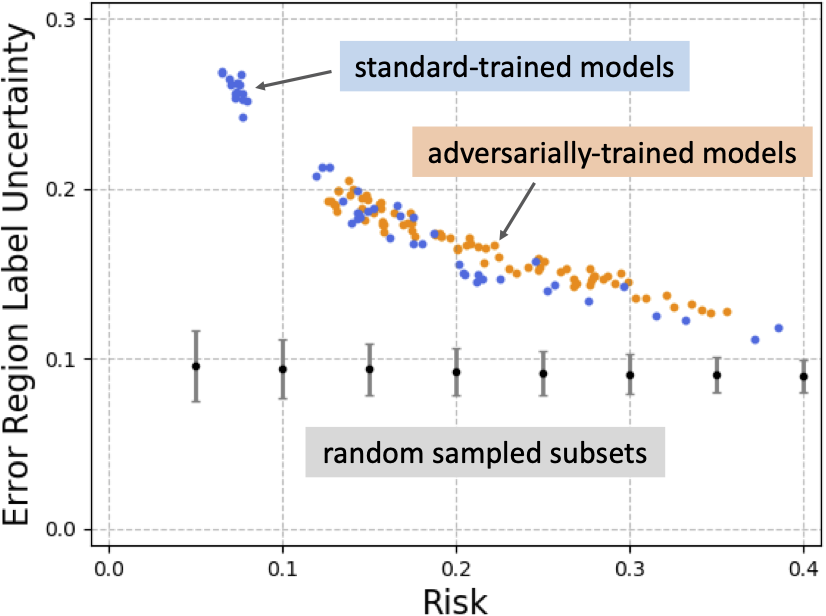
In this work, we argue that the standard concentration of measure problem is not sufficient to capture a realistic intrinsic robustness limit for a classification problem. In particular, the standard concentration function is defined as an inherent property regarding the input metric probability space, which does not take account of the underlying label information. However, such label information is essential for any supervised learning problem, including adversarially robust classification, so must be incorporated into intrinsic robustness limits. By introducing a novel definition of label uncertainty, which characterizes the average uncertainty of label assignments for an input region, we empirically demonstrate that error regions induced by state-of-the-art models tend to have much higher label uncertainty than randomly-selected subsets.
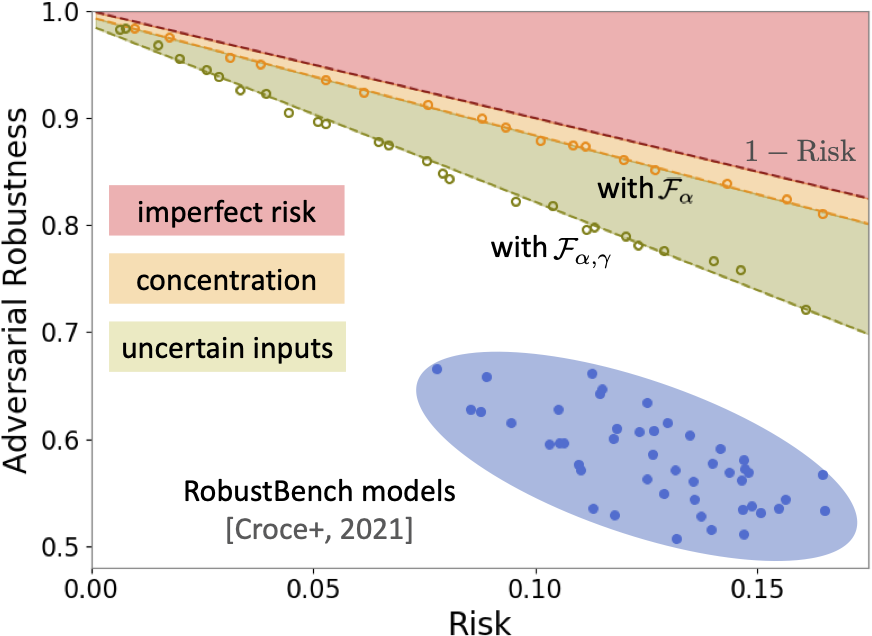
This observation motivates us to adapt a concentration estimation algorithm to account for label uncertainty, where we focus on understanding the concentration of measure phenomenon with respect to input regions with label uncertainty exceeding a certain threshold $\gamma>0$. The intrinsic robustness estimates we obtain by incorporating label uncertainty (shown as the green dots in the figure below) are much lower than prior limits, suggesting that compared with the concentration of measure phenomenon, the existence of uncertain inputs may explain more fundamentally the adversarial vulnerability of state-of-the-art robustly-trained models.
Paper: Xiao Zhang and David Evans. Understanding Intrinsic Robustness Using Label Uncertainty. In Tenth International Conference on Learning Representations (ICLR), April 2022. [PDF] [OpenReview] [ArXiv]
Code: https://github.com/xiaozhanguva/intrinsic_rob_lu