Our research seeks to empower individuals and organizations to control how their data is used. We use techniques from cryptography, programming languages, machine learning, operating systems, and other areas to both understand and improve the privacy and security of computing as practiced today, and as envisioned in the future. A major current focus is on adversarial machine learning.
Inference Privacy
Security ML
Auditing ML Systems
Congratulations, Dr. Suri!
Steering the CensorShip

Orthodoxy means not thinking—not needing to think.
(George Orwell, 1984)
Uncovering Representation Vectors for LLM ‘Thought’ Control
Hannah Cyberey’s blog post summarizes our work on controlling the censorship imposed through refusal and thought suppression in model outputs.
Paper: Hannah Cyberey and David Evans. Steering the CensorShip: Uncovering Representation Vectors for LLM “Thought” Control. 23 April 2025.
Demos:
-
🐳 Steeing Thought Suppression with DeepSeek-R1-Distill-Qwen-7B (this demo should work for everyone!)
-
🦙 Steering Refusal–Compliance with Llama-3.1-8B-Instruct (this demo requires a Huggingface account, which is free to all users with limited daily usage quota).
Code: https://github.com/hannahxchen/llm-censorship-steering
US v. Google
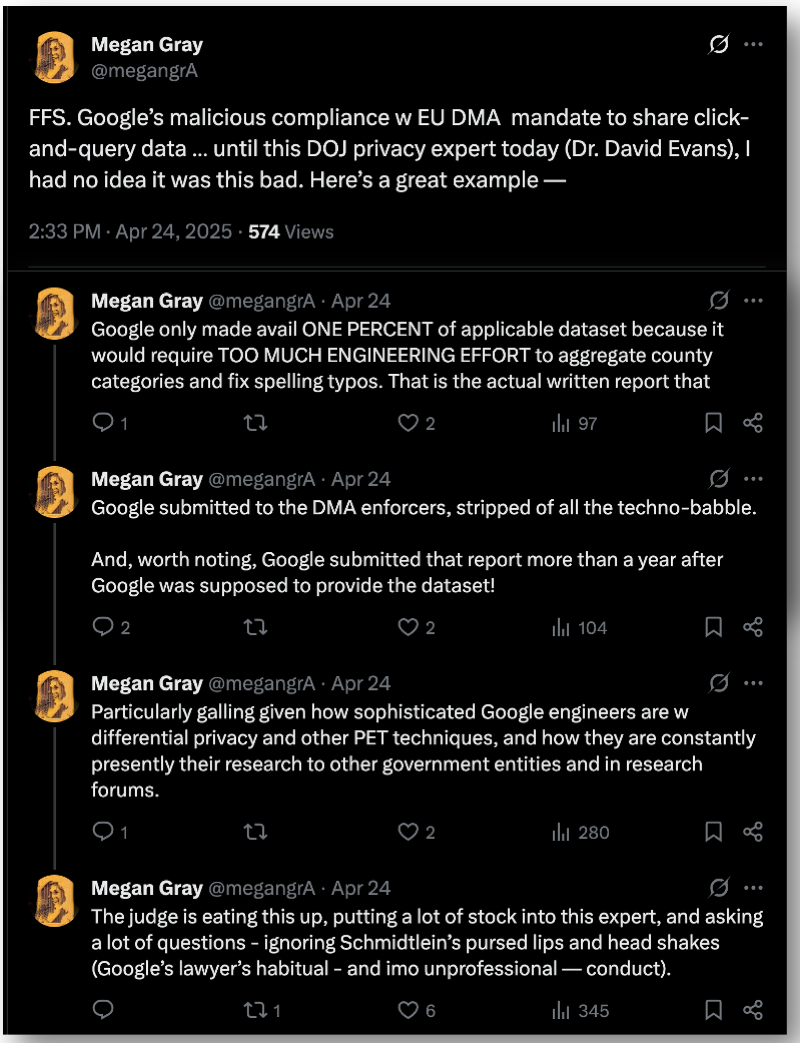
Now that I’ve testified as an Expert Witness on Privacy for the US (and 52 state partners), I can share some links about US v. Google. (I’ll wait until the judgement before sharing any of my own thoughts other than to say it was a great experience and a priviledge to be able to be part of this.)
The Department of Justice Website has public posts of many trial materials, including my demonstrative slides (with only one redaction).
We are now done w the DOJ privacy expert (Dr. David Evans). It was his first time as a testifying expert and he knocked it out of the park. Kudos!
— Megan Gray (@megangrA) April 24, 2025
Weird Google cross of this DOJ privacy expert — Google is just giving judge a roadmap on improving the order in way that DOJ would support. Like, Google is putting more meat on a bone that Google wants to the judge to throw away.
— Megan Gray (@megangrA) April 24, 2025
This article has the most detailed and accurate account I’ve seen so far: Google Case Judge Weighs Rivals’ Data Needs Against Privacy [PDF]
New Classes Explore Promise and Predicaments of Artificial Intelligence
The Docket (UVA Law News) has an article about the AI Law class I’m helping Tom Nachbar teach:
New Classes Explore Promise and Predicaments of Artificial Intelligence
Attorneys-in-Training Learn About Prompts, Policies and Governance
The Docket, 17 March 2025
Nachbar teamed up with David Evans, a professor of computer science at UVA, to teach the course, which, he said, is “a big part of what makes this class work.”
“This course takes a much more technical approach than typical law school courses do. We have the students actually going in, creating their own chatbots — they’re looking at the technology underlying generative AI,” Nachbar said. Better understanding how AI actually works, Nachbar said, is key in training lawyers to handle AI-related litigation in the future.
“I want my students to have a solid understanding about what’s actually happening under the hood, as it were, so that when they confront a case, they know what kinds of questions to start asking,” he said.
Tom and I will co-teach a jointly-listed Law and Computer Science AI Law class in the fall.
Is Taiwan a Country?
I gave a short talk at an NSF workshop to spark research collaborations between researchers in Taiwan and the United States. My talk was about work Hannah Cyberey is leading on steering the internal representations of LLMs:

Steering around Censorship
Taiwan-US Cybersecurity Workshop
Arlington, Virginia
3 March 2025



 University of Virginia
University of Virginia 