Post by Katherine Knipmeyer
Machine learning poses a substantial risk that adversaries will be able to discover information that the model does not intend to reveal. One set of methods by which consumers can learn this sensitive information, known broadly as membership inference attacks, predicts whether or not a query record belongs to the training set. A basic membership inference attack involves an attacker with a given record and black-box access to a model who tries to determine whether said record was a member of the model’s training set.
Unlike much of the existing research on the membership inference, though, these particular results focus on what are considered “realistic assumptions,” including conditions with skewed priors (wherein members only make up a small fraction of the candidate pool) and conditions with adversaries that select accuracy-improving inference thresholds based on specific attack goals. These new assumptions help to answer the question of how differential privacy can be implemented to provide meaningful privacy guarantees in practice.
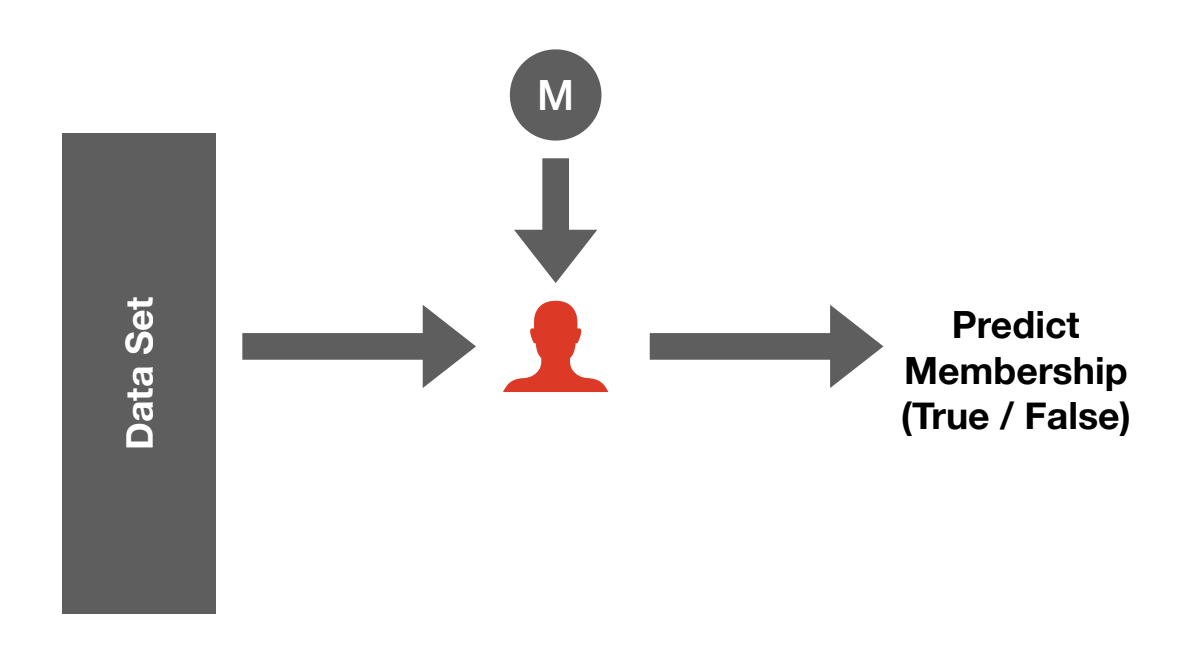
Threshold Selection
In order to classify a record as either a member or a non-member, there must be a threshold that converts a real number output from a test into a Boolean. We develop a procedure to select a threshold, φ, that allows the adversary to achieve as much privacy leakage as possible while staying beneath a maximum false positive rate, α.
This selection procedure can be applied to any membership inference attack, including Yeom’s attack. The original version of this attack classifies a record as a member if its per-instance-loss is less than the expected training loss, whereas this new approach selects members based on a threshold φ, which can be set to target a particular false positive rate.
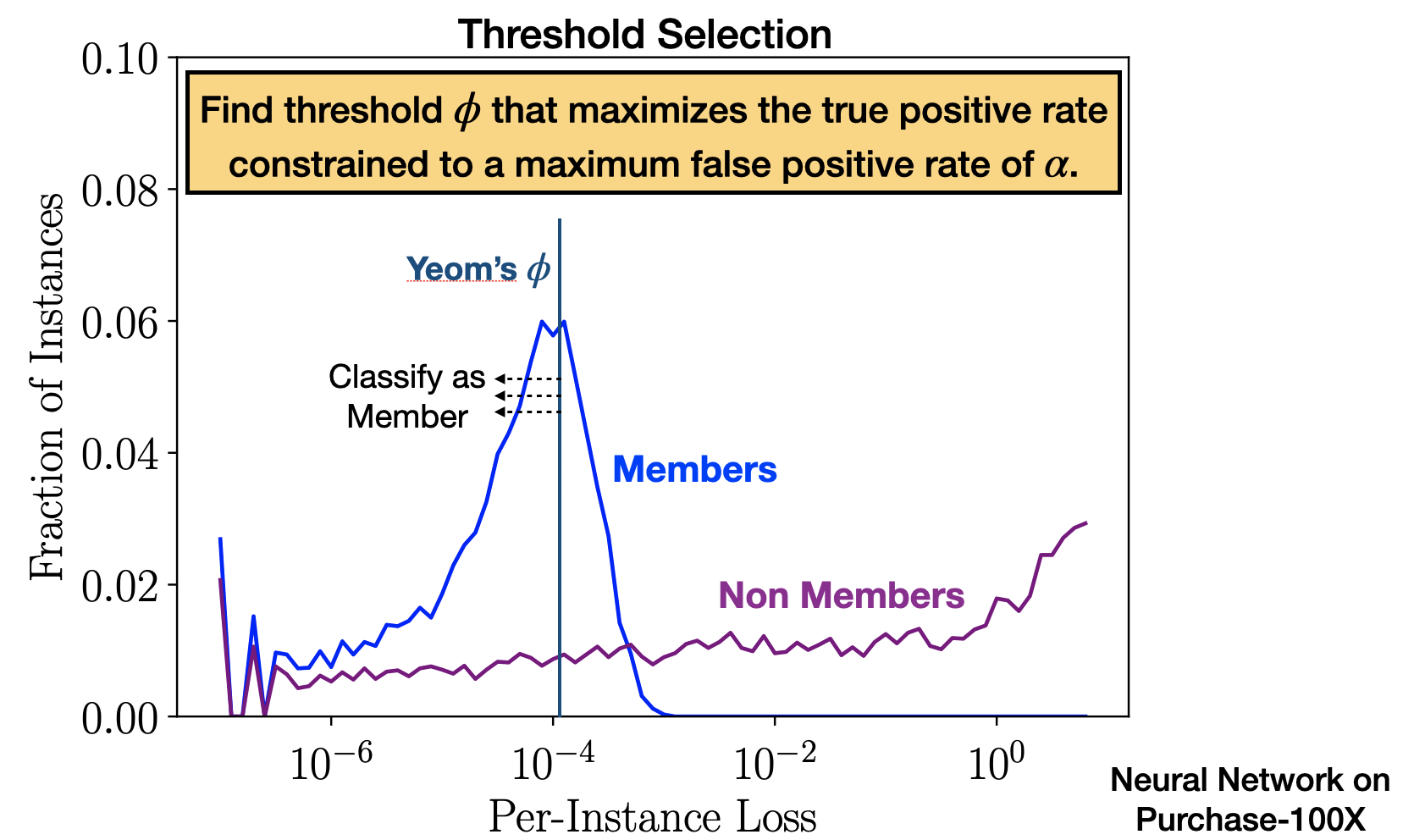
The Merlin Attack
In addition to this new selection procedure, we introduce a new attack known as Merlin, which stands for MEasuring Relative Loss In Neighborhood. Instead of per-instance-loss, this attack uses the direction of change of per-instance-loss when the record is slightly perturbed with noise. Merlin operates based on the intuition that, as a result of overfitting, member records are more likely to be near local minima than non-member records. This suggests that for members, loss is more likely to increase at perturbed points near the original, whereas it is equally likely to increase or decrease for non-members. For each record, a small amount of random Gaussian noise is added and the change of loss direction is recorded. This process is repeated multiple times and Merlin infers membership based on the fraction of times the loss increases.
The Morgan Attack
Since Yeom and Merlin use different information to make their membership inferences, they do not always identify the same records as members; some members are more vulnerable to one attack than the other. Visualizing a combination of the attacks’ results suggests that by eliminating the results with a very low per-instance-loss, a combination of the two may produce an improved PPV. The intuition here is that extremely low per-instance-losses may result in Merlin’s identification of a local minimum where there is in fact a near global minimum (which is much less strongly correlated with membership).
The Morgan (Measuring lOss, Relatively Greater Around Neighborhood) attack uses three different thresholds: a lower threshold on per-instance loss (φL), an upper threshold on per-instance loss (φU), and a threshold on the ratio as used by Merlin (φM). If a record has a per-instance-loss that falls between φL and φU, and has a Merlin ratio of at least φM, Morgan identifies it as a member.
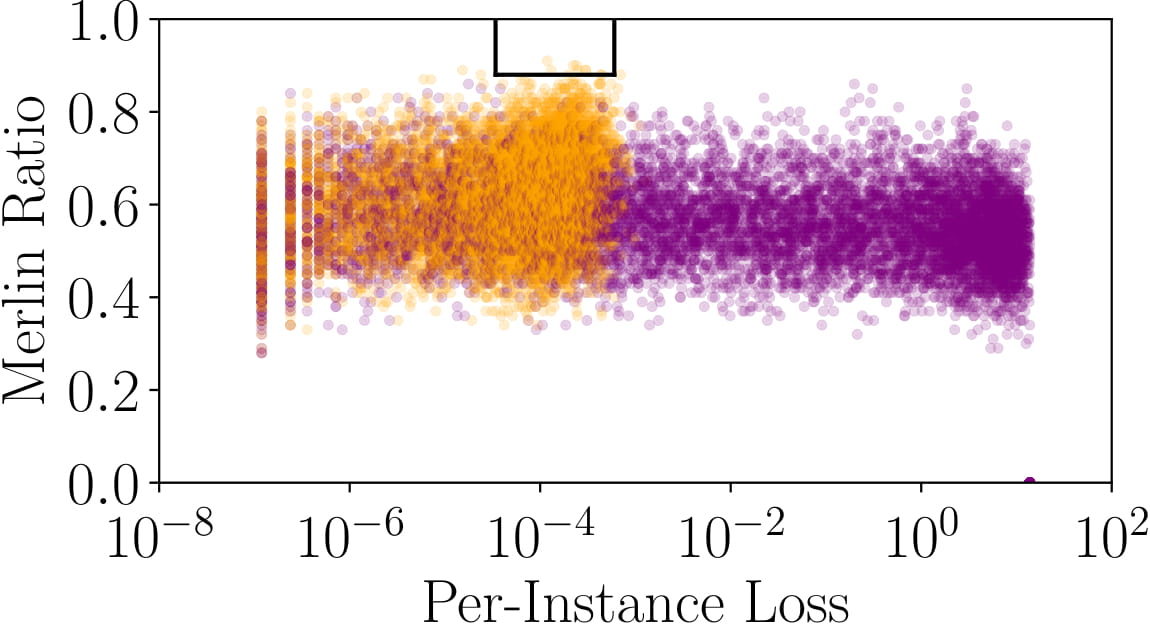
The figure shows the per-instance loss and Merlin ratio for Purchase-100X (and expanded version of the Purchase-100 dataset that we created for our experiments). Members and nonmembers are denoted by orange and purple points respectively. The boxes show the thresholds found by the threshold selection process (without access to the training data, but with the same data distribution), and illustrate the regions where members are identified by Morgan with very high confidence (PPV ∼1). (See paper for details, and more result.)
Imbalanced Priors
Previous work on membership inference attacks assumes a candidate pool where half of the candidates are members. For most settings, especially ones where there is a serious privacy risk for an individual of being identified as a dataset member, this assumption is unrealistic. It is important to understand how well inference attacks work when the adversary’s candidate pool has a different prior probability of being amember.
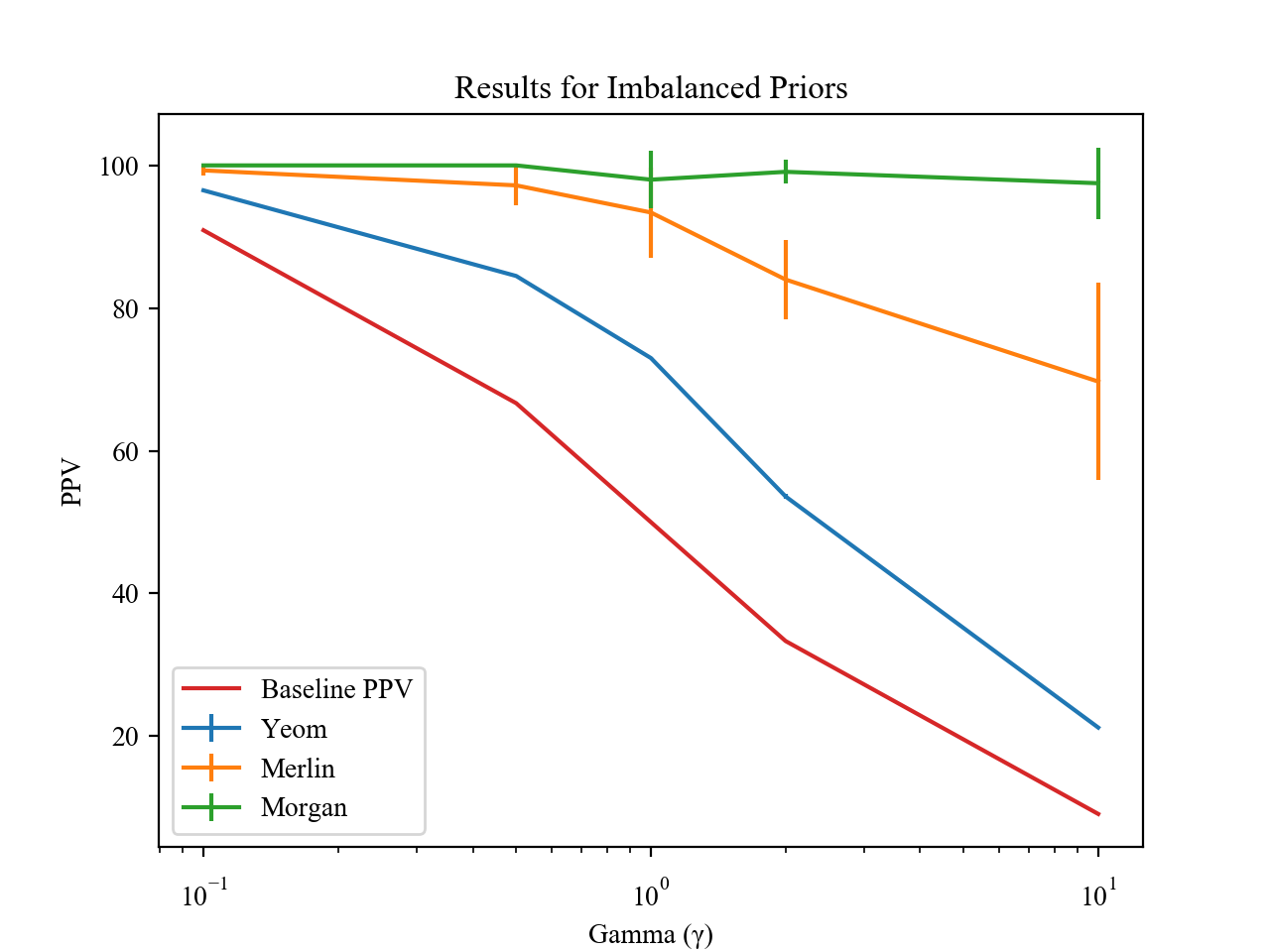
Here, the candidate pool from which the attacker attempts to select members has γ times more non-member records than member records. As shown above, even in situations that other papers do not consider, wherein there are many times more non-members than members, attacks are able to attain a high rate of positively-identified members.
Conclusion
The Merlin and Morgan attacks can reliably identify members even in situations with imbalanced priors where other attacks fail to show meaningful inference risk.
There remains a large gap between what can be guaranteed using differential privacy methods, and what can be inferred using known inference attacks. This means better inference attacks may exist, and our results show that there are concrete ways to improve attacks (e.g., our threshold-selection procedure) and to incorporate more information to improve attacks. We are especially interested in attacks that produce extremely high PPVs, even if this is only for a small fraction of candidates, since for most scenarios this is where the most serious privacy risks lie.
Full paper: Bargav Jayaraman, Lingxiao Wang, Katherine Knipmeyer, Quanquan Gu, David Evans. Revisiting Membership Inference Under Realistic Assumptions (arXiv).