(Cross-post by Anshuman Suri)
Inference attacks seek to infer sensitive information about the training process of a revealed machine-learned model, most often about the training data.
Standard inference attacks (which we call “dataset inference attacks”) aim to learn something about a particular record that may have been in that training data. For example, in a membership inference attack (Reza Shokri et al., Membership Inference Attacks Against Machine Learning Models, IEEE S&P 2017), the adversary aims to infer whether or not a particular record was included in the training data.
Differential Privacy provides a theoretical notion of privacy that maps well to membership inference attacks. However, it provides privacy at the dataset level. Thus, it doesn’t capture attacks that violate privacy at the distribution level. This is where property inference comes in. Property inference, a different kind of inference risk, involves an adversary that aims to infer some statistical property of the training distribution.
We illustrate the kind of risks introduced by property inference via a fictional example. Skynet, an (imaginary) organization that handles private data, releases a machine learning model $M$ trained on their network flow graphs to predict faulty nodes in a network of servers. However, an adversary ($\mathcal{A}$) that wishes to launch a bot-net into this cluster of servers sees an opportunity in this model. They seek to infer whether the effective diameter ($90^{th}$ percentile of all pair-wise shortest paths) of the network is below 6 ($\mathcal{D}_0$) or not ($\mathcal{D}_1$).
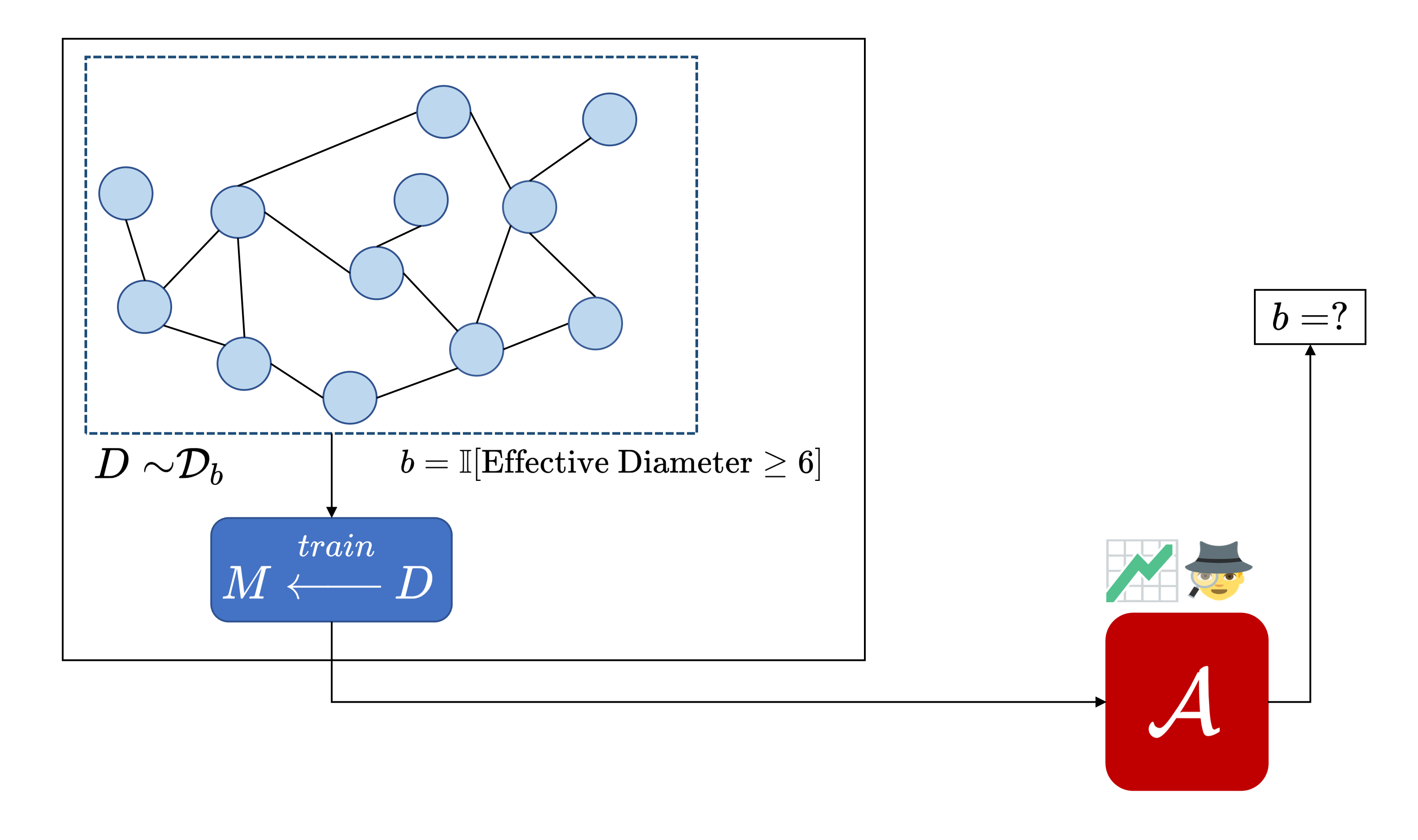
We picked this property as an example based on useful properties cited in the traffic classification literature (e.g., Iliofotou, et al.). Learning this property might be useful for the adversary in crafting a bot-net that would not be detected by Skynet’s bot-detection software. The main point of the illustration is to convey that an adversary can infer properties of the underlying data distribution that a model producer would not expect and that might be valuable to the adversary.
Formalizing Property Inference
To formalize property inference attacks, we adapt the cryptographic game for membership inference proposed by Yeom et al. (Privacy Risk in Machine Learning: Analyzing the Connection to Overfitting, CSF 2018):
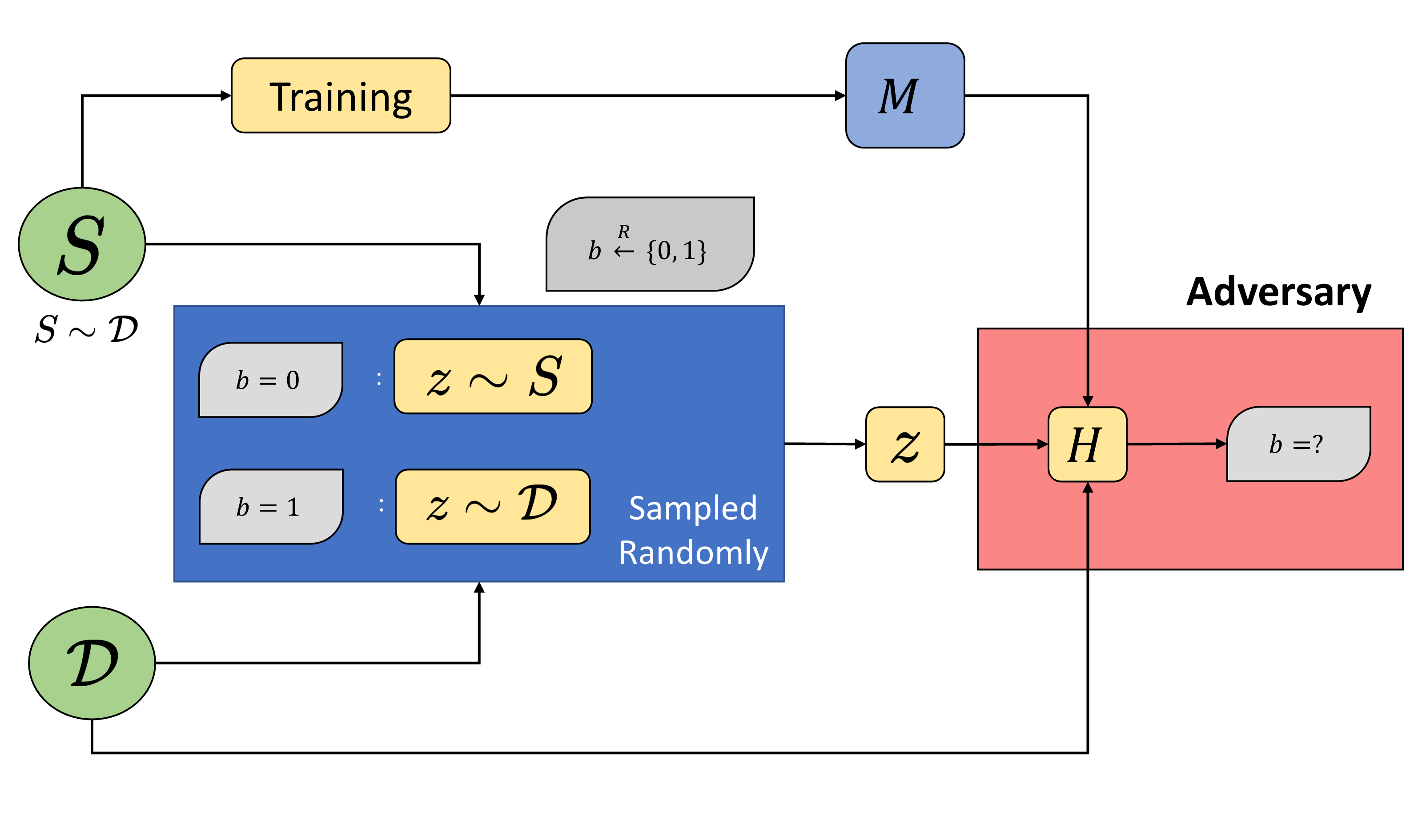
In this game, the victim samples a dataset S from the distribution $\mathcal{D}$ and trains a model $M$ on it. It then samples some data-point $z$ from either $S$ or $\mathcal{D}$, based on $b \xleftarrow{R}${0,1}. The adversary then tries to infer $b$ using algorithm $H$, given access to ($z$, $\mathcal{D}$, $M$). This cryptographic game captures the intuitive notion of membership inference. It focuses on a particular dataset and sample: inferring whether a given data point was part of training data.
In contrast, property inference focuses on properties of the underlying distribution ($\mathcal{D}$), not the dataset ($S$) itself. To capture property inference, we propose a similar cryptographic game. Instead of differentiating between the sources of a specific data point ($S$ or $\mathcal{D}$), we propose distinguishing between two distributions, $\mathcal{D}_0$ and $\mathcal{D}_1$.
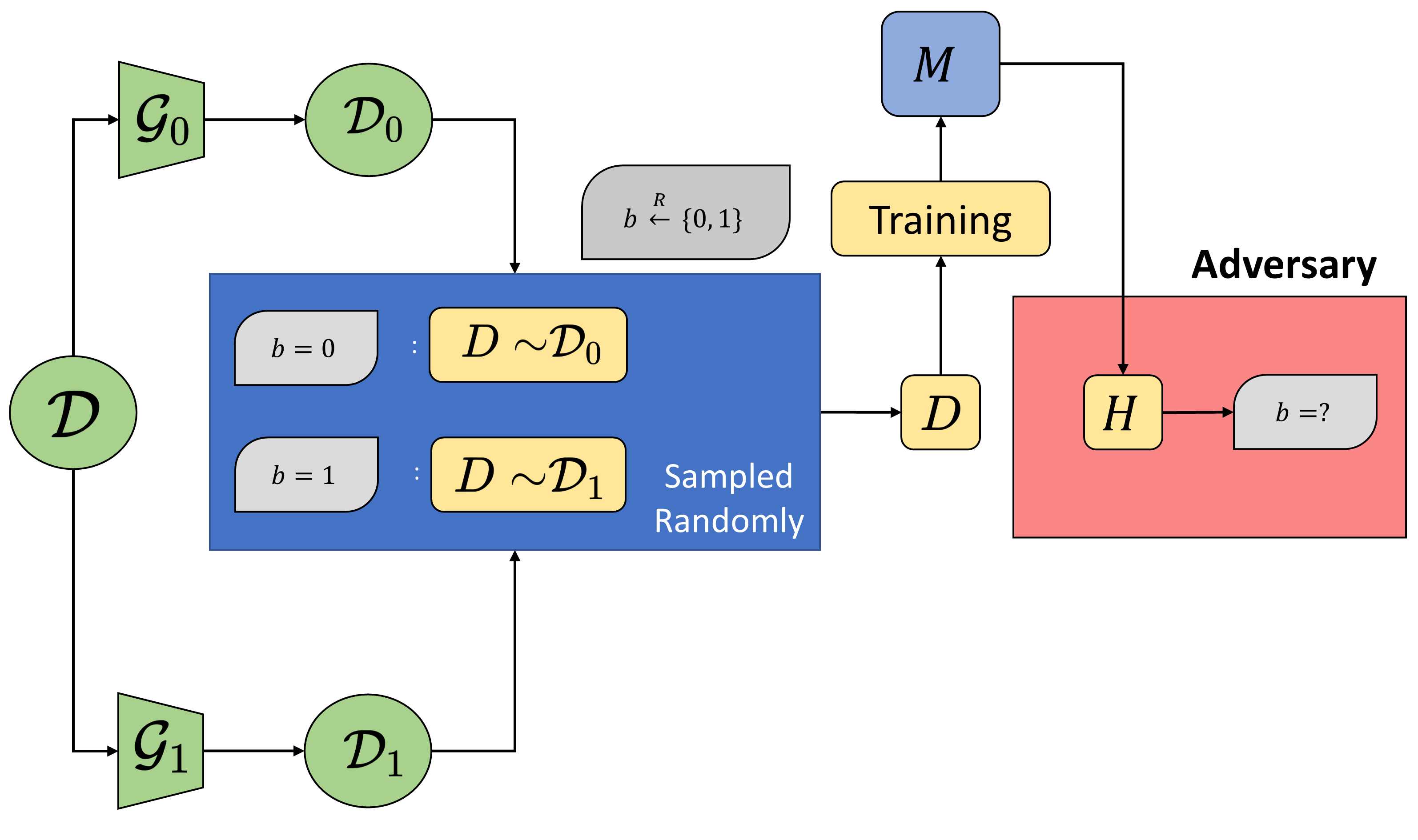
A model trainer $\mathcal{B}$ samples a dataset $D$ from either of the distributions $\mathcal{D}_0$, $\mathcal{D}_1$. These distributions can be obtained from the publicly know distribution $\mathcal{D}$ by applying functions $\mathcal{G}_0$, $\mathcal{G}_1$ respectively, that transform distributions (and represent the “property” an adversary might care about). So, we formalize distribution inference with this question:
Frameworks like Differential Privacy do not apply here: the adversary here cares about statistical properties of the distribution the model was trained on, not details about a particular sampled dataset.
Evaluating Risk of Property Inference
Most often in the literature, the adversary considers the ratio of members in a dataset satisfying a particular Boolean function $f$ as the “property.” It then aims to distinguish between models trained on datasets with different proportions.
However, these experiments often test with arbitrary ratios, making it hard to understand the relative risk of different properties. Some examples are Melissa Chase et al., Property Inference From Poisoning (which considers 0.1 v/s 0.25) and Wanrong Zhang et al., Leakage of Dataset Properties in Multi-Party Machine Learning (which considers 0.33 v/s 0.67).
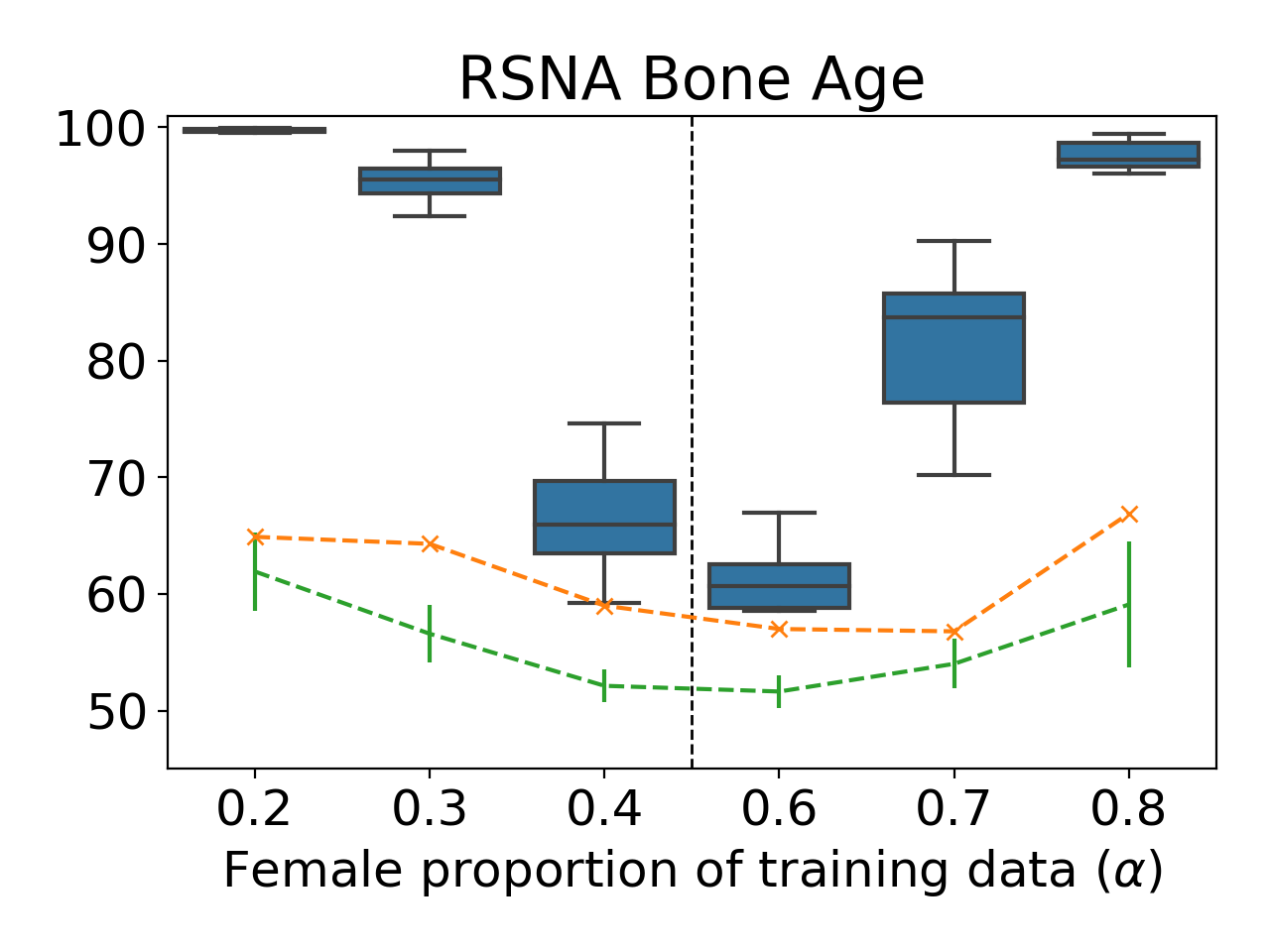
To better understand how well an intuitive notion of divergence in properties aligns with observed inference risk, we execute property inference attacks with increasing diverging properties. We fix one property (ratio=0.5) and vary the other ($\alpha$). We perform these experiments for three datasets: focusing on the ratio of females for the US Census and RSNA BoneAge datasets, and the average node-degree for the OGBN arXiv dataset.
The state-of-the-art method for property inference attacks involves meta-classifiers, usually using Permutation Invariant Networks (Karan Ganju et al., Property Inference Attacks on Fully Connected Neural Networks using Permutation Invariant Representations). After training hundreds or thousands of models locally, the adversary trains a meta-classifier on model parameters.
Illustration of the functioning of a Permutation Invariant Network. The process of model-parameter extraction involves constructing permutation-invariant representations of neurons per layer $h_i$ using learnable parameters ($\phi_i$). These representations are then joined together for all layers with another learnable transform $\rho$, yielding the meta-classifier’s predictions.
We use two simple attacks (using only model outputs) as baselines:
- Loss Test: predict the property based on its performance on data from the same distribution it was trained, compared to the other distribution being analyzed.
- Threshold Test: extends the loss test by calibrating performance trends on a small set of models and arriving at a threshold based on model performance.
Experimental Results
Our results demonstrate how a meta-classifier can differentiate between models with ratios as similar as 0.5 and 0.6:
 |
 |
The meta-classifier attacks provide the best predictions, but the loss-test and threshold-test can serve as valuable baselines — even these simple attacks provide accuracies significantly better than random-guessing.
Inferring Graph Properties
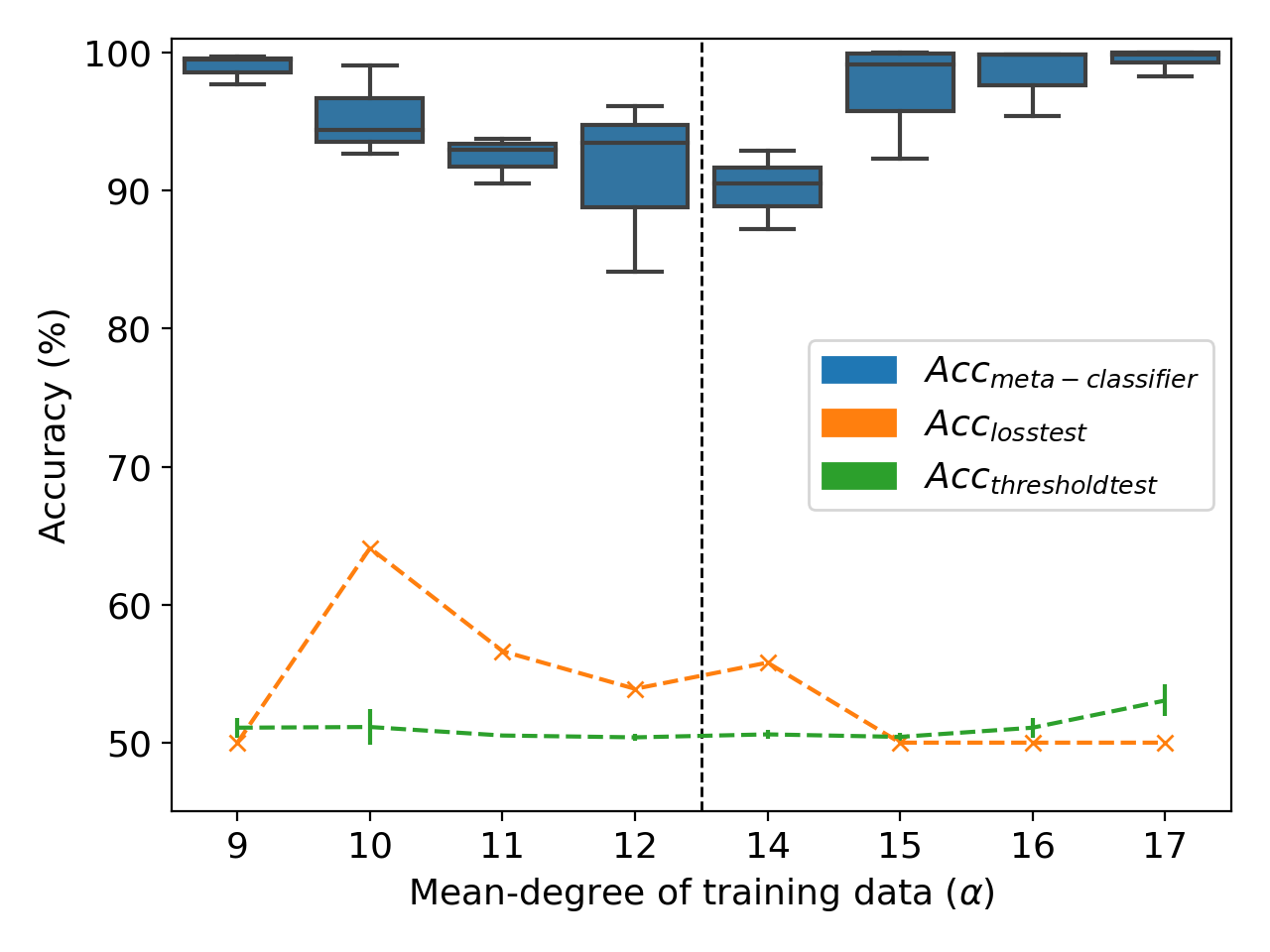
Our proposed definitions allow the property to hold over the whole dataset, not just aggregate statistics like mean ratio. Thus, we focus on node-classification for a graph: differentiating between versions of the graph with varying mean node-degrees as the property. We fix one property (mean node-degree 13) and vary the other ($\alpha$). Inferring the mean node-degree is a novel property inference task since the property here holds over the entirety of training data- no such property has been explored in the literature yet.
 |
 |
|
Figure 2: Differentiating between models trained on datasets trained with mean node-degree 13 v/s on the OGBN arXiv dataset.
|
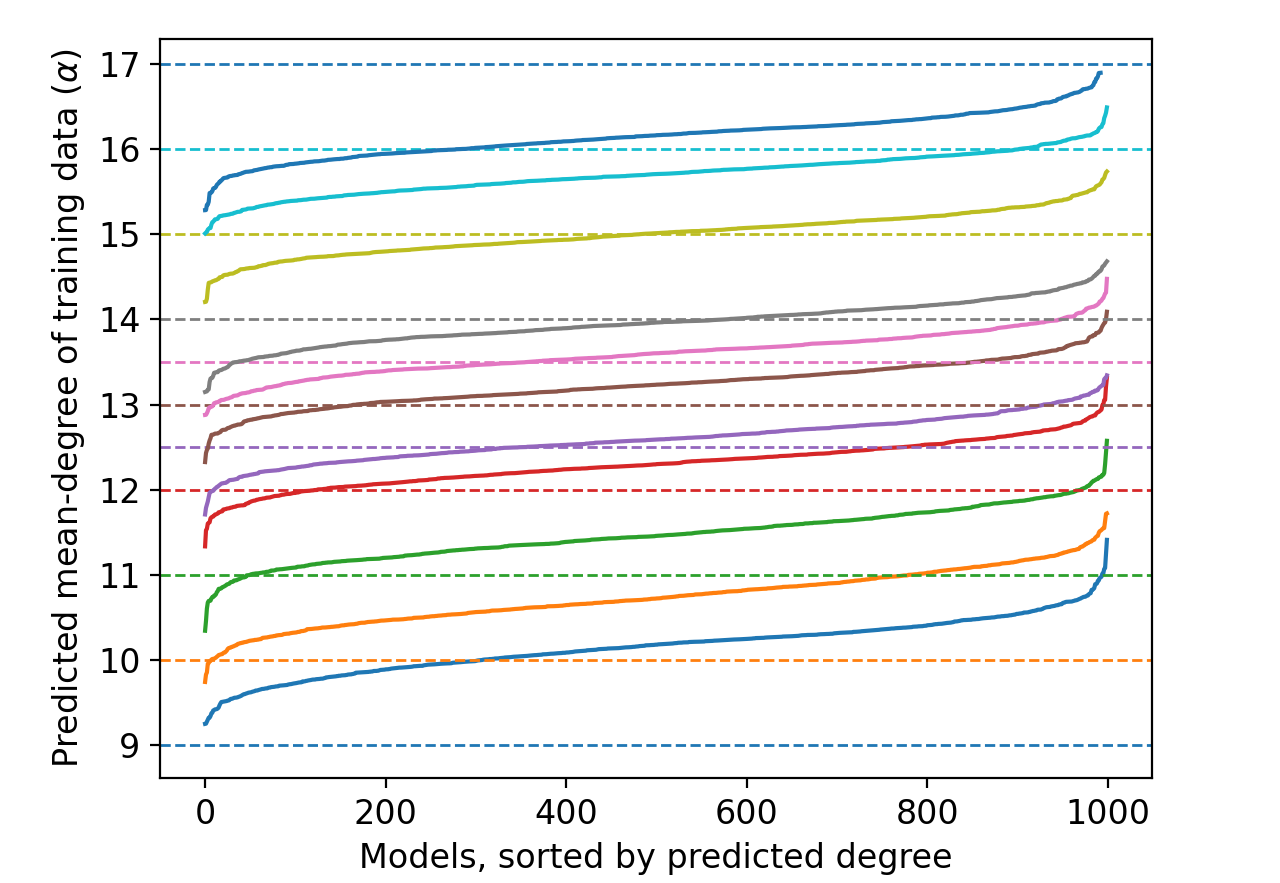
Figure 3: Predicting the mean node-degree of training data graphs directly with a meta-classifier on the OGBN arXiv dataset.
|
Our results demonstrate how a meta-classifier can also be trained to directly infer the mean-node degree of graphs (Figure 2). Encouraged by the success of meta-classifiers for this task, we also tried a meta-classifier variant to predict the mean-node degree of training graphs (Figure 3). The resulting meta-classifier even generalizes well, accurately predicting mean node-degrees for distributions ($\alpha$={12.5, 13.5}) that it hasn’t seen.
Summary
Our work on distribution inference formalizes and shows how property inference attacks can indeed infer distribution-level properties. Our ongoing work is focused on quantifying and studying this ‘privacy leakage’ of properties and its implications.
Pre-print: Anshuman Suri, David Evans. Formalizing Distribution Inference Risks (arXiv).
A more detailed and updated paper is now available: Formalizing and Estimating Distribution Inference Risks (arXiv).