(Cross-post by Anshuman Suri)
Distribution inference attacks aims to infer statistical properties of data used to train machine learning models. These attacks are sometimes surprisingly potent, as we demonstrated in previous work.
KL Divergence Attack
Most attacks against distribution inference involve training a meta-classifier, either using model parameters in white-box settings (Ganju et al., Property Inference Attacks on Fully Connected Neural Networks using Permutation Invariant Representations, CCS 2018), or using model predictions in black-box scenarios (Zhang et al., Leakage of Dataset Properties in Multi-Party Machine Learning, USENIX 2021). While other black-box were proposed in our prior work, they are not as accurate as meta-classifier-based methods, and require training shadow models nonetheless (Suri and Evans, Formalizing and Estimating Distribution Inference Risks, PETS 2022).
We propose a new attack: the KL Divergence Attack. Using some sample of data, the adversary computes predictions on local models from both distributions as well as the victim’s model. Then, it uses the prediction probabilities to compute KL divergence between the victim’s models and the local models to make its predictions. Our attack outperforms even the current state-of-the-art white-box attacks.
We observe several interesting trends across our experiments. One striking example is that with varying task-property correlation. While intuition suggests increasing inference leakage with increasing correlation between the classifier's task and the property being inferred, we observe no such trend:
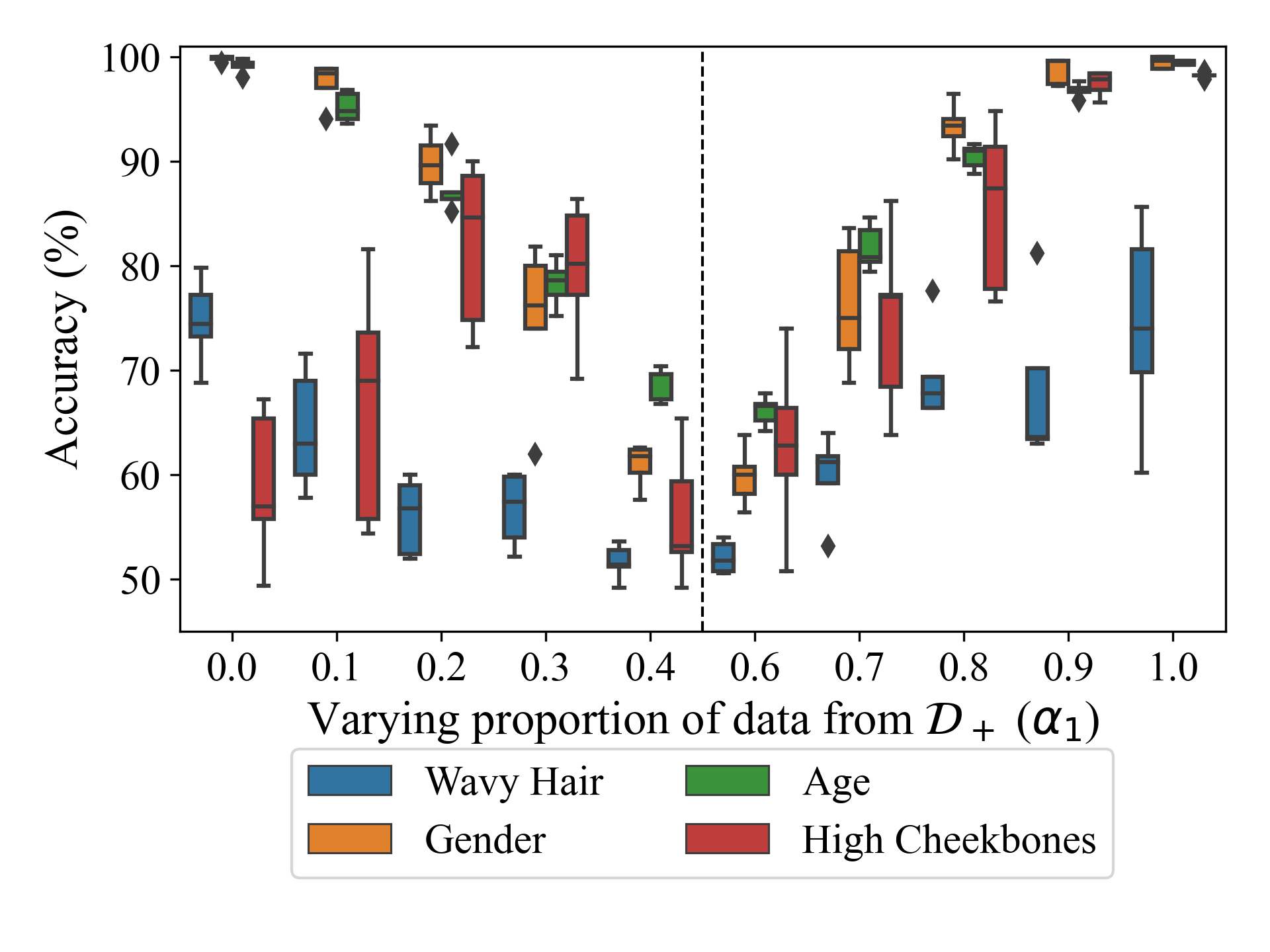
Impact of adversary’s knowledge
We evaluate inference risk while relaxing a variety of implicit assumptions of the adversary;s knowledge in black-box setups. Concretely, we evaluate label-only API access settings, different victim-adversary feature extractors, and different victim-adversary model architectures.
| Victim Model | Adversary Model | |||
|---|---|---|---|---|
| RF | LR | MLP$_2$ | MLP$_3$ | |
| Random Forest (RF) | 12.0 | 1.7 | 5.4 | 4.9 |
| Linear Regression (LR) | 13.5 | 25.9 | 3.7 | 5.4 |
| Two-layer perceptron (MLP$_2$) | 0.9 | 0.3 | 4.2 | 4.3 |
| Three-layer perceptron (MLP$_3$) | 0.2 | 0.3 | 4.0 | 3.8 |
Consider inference leakage for the Census19 dataset (table above with mean $n_{leaked}$ values) as an example. Inference risk is significantly higher when the adversary uses models with learning capacity similar to the victim, like both using one of (MLP$_2$, MLP$_3$) or (RF, MLP). Interestingly though, we also observe a sharp increase in inference risk when the victim uses models with low capacity, like LR and RF instead of multi-layer perceptrons.
Defenses
Finally, we evaluate the effectiveness of some empirical defenses, most of which add noise to the training process.
For instance while inference leakage reduces when the victim utilizes DP, most of the drop in effectiveness comes from a mismatch in the victim’s and adversary’s training environments:
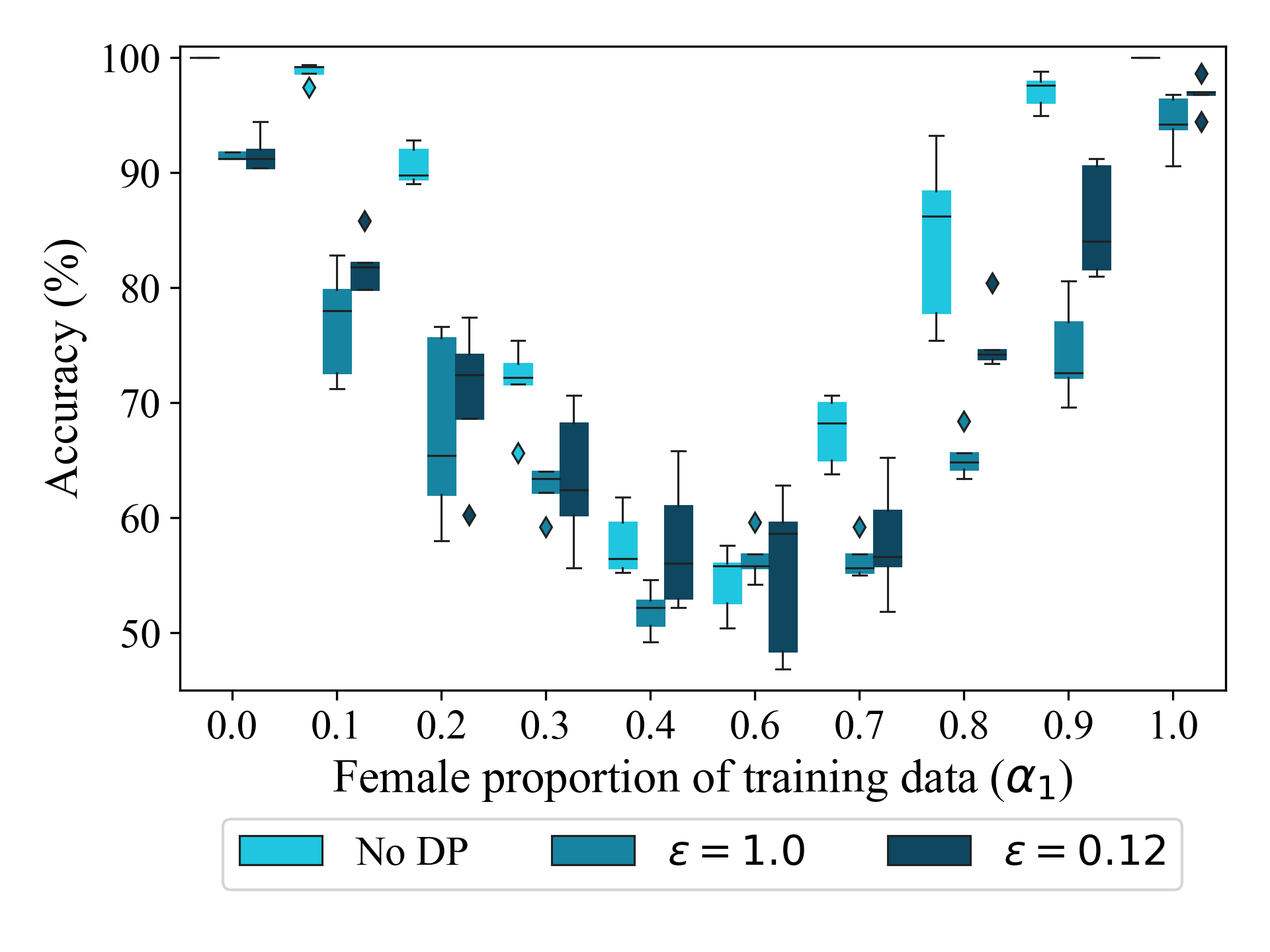
Compared to an adversary that does not use DP, there is a clear increase in inference risk (mean $n_{leaked}$ increases to 2.9 for $\epsilon=1.0$, and 4.8 for $\epsilon=0.12$ compared to 4.2 without any DP noise).
Our exploration of potential defenses also reveals a strong connection between model generalization and inference risk (as apparent below, for the case of Celeb-A), suggesting that the defenses that do seem to work are attributable to poor model performance, and not something special about the defense itself (like adversarial training or label noise).
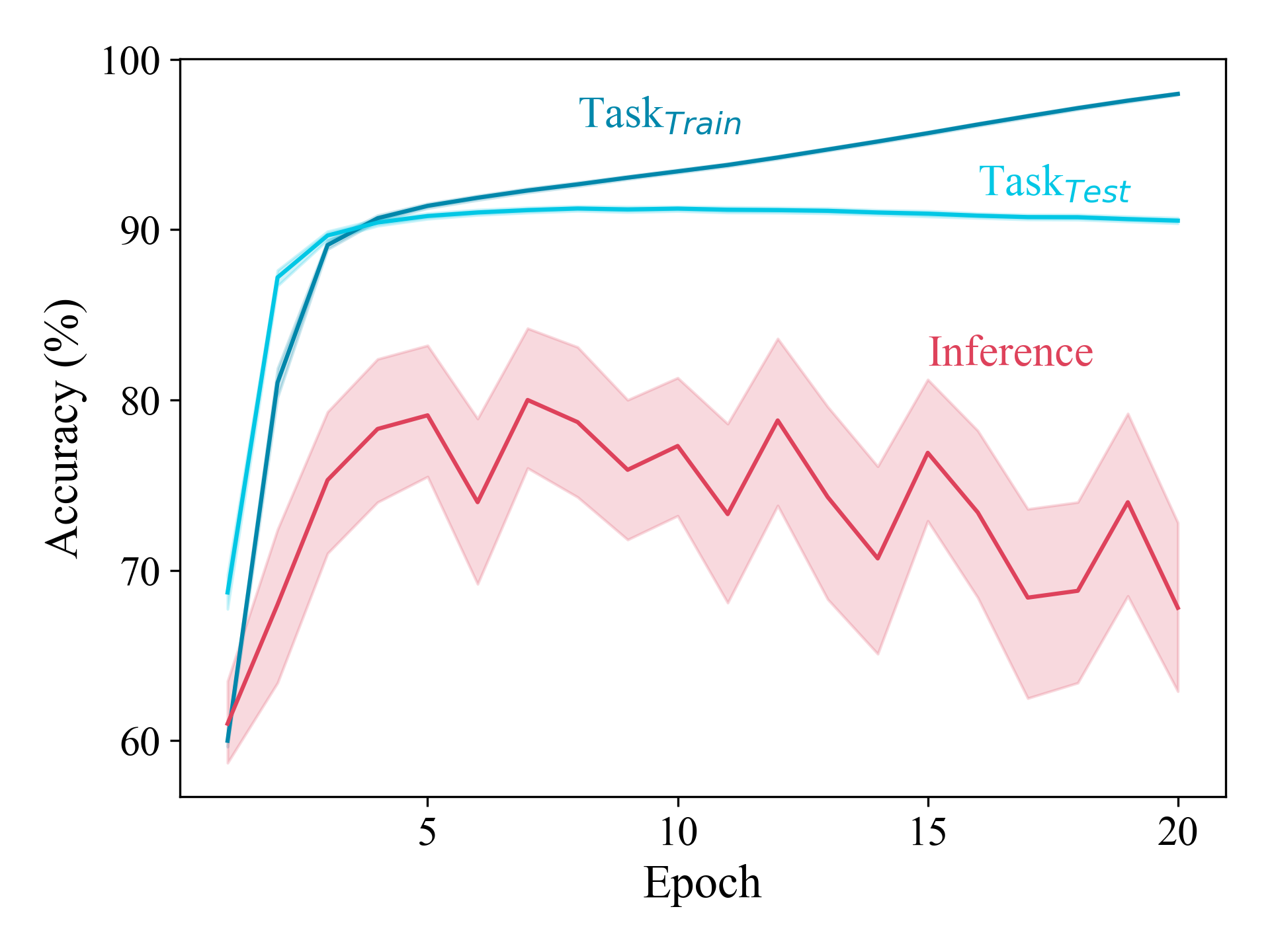
Summary
The general approach to achieve security and privacy for machine-learning models is to add noise, but our evaluations suggest this approach is not a principled or effective defense against distribution inference. The main reductions in inference accuracy that result from these defenses seem to be due to the way they disrupt the model from learning the distribution well.
Paper: Anshuman Suri, Yifu Lu, Yanjin Chen, David Evans. Dissecting Distribution Inference. In IEEE Conference on Secure and Trustworthy Machine Learning (SaTML), 8-10 February 2023.
Code: https://github.com/iamgroot42/dissecting_distribution_inference