Anshuman Suri’s talk at IEEE Conference on Secure and Trustworthy Machine Learning (SaTML) is now available:
See the earlier blog post for more on the work, and the paper at https://arxiv.org/abs/2310.17534.
Our research seeks to empower individuals and organizations to control how their data is used. We use techniques from cryptography, programming languages, machine learning, operating systems, and other areas to both understand and improve the privacy and security of computing as practiced today, and as envisioned in the future. A major current focus is on adversarial machine learning.
Everyone is welcome at our research group meetings. To get announcements, join our Teams Group (any @virginia.edu email address can join themsleves; others should email me to request an invitation).
Privacy for Machine Learning
Security for Machine Learning
Auditing ML Systems
Web and Mobile Security: ScriptInspector ·
SSOScan
Program Analysis: Splint · Perracotta
N-Variant Systems ·
Physicrypt ·
More…
Anshuman Suri’s talk at IEEE Conference on Secure and Trustworthy Machine Learning (SaTML) is now available:
See the earlier blog post for more on the work, and the paper at https://arxiv.org/abs/2310.17534.

Congratulations to Josephine Lamp for successfully defending her PhD thesis!
The explosion of medical sensors and wearable devices has resulted in the collection of large amounts of medical trajectories. Medical trajectories are time series that provide a nuanced look into patient conditions and their changes over time, allowing for a more fine-grained understanding of patient health. It is difficult for clinicians and patients to effectively make use of such high dimensional data, especially given the fact that there may be years or even decades worth of data per patient. Clinical Decision Support Systems (CDSS) provide summarized, filtered, and timely information to patients or clinicians to help inform medical decision-making processes. Although CDSS have shown promise for data sources such as tabular and imaging data, e.g., in electronic health records, the opportunities of CDSS using medical trajectories have not yet been realized due to challenges surrounding data use, model trust and interpretability, and privacy and legal concerns.
This dissertation develops novel machine learning frameworks for trustworthy CDSS using medical trajectories. We define trustworthiness in terms of three desiderata: (1) robust—providing reliable outputs from the CDSS even when inputs are variable, irregular or missing; (2) explainable—providing understandable, actionable explanations for CDSS predictions to clinicians or patients; and (3) privacy-preserving—providing CDSS that use data without violating patients’ privacy expectations. We develop interpretable machine learning frameworks that are robust to missing, irregular, variable and conflicting trajectories that directly address data and model challenges. Moreover, we develop privacy-preserving learning methodologies that allow for the safe sharing and aggregation of medical trajectories and directly address privacy challenges. We evaluate our frameworks across a wide selection of benchmarks and show that our techniques can learn valuable insights from trajectory data with high accuracy and strong privacy guarantees.
Dissertation: Trustworthy Clinical Decision Support Systems for Medical Trajectories
Committee:
Lu Feng, Co-Advisor (UVA Computer Science)
David Evans, Co-Advisor (UVA Computer Science)
Tianhao Wang, Committee Chair (CS/SEAS/UVA)
Miaomiao Zhang (ECE,CS/SEAS/UVA)
Rich Nguyen (CS/SEAS/UVA)
Sula Mazimba (School of Medicine, Cardiovascular Medicine/UVA)
Tingting Zhu (Engineering Science, University of Oxford)

Membership inference attacks (MIAs) attempt to predict whether a particular datapoint is a member of a target model’s training data. Despite extensive research on traditional machine learning models, there has been limited work studying MIA on the pre-training data of large language models (LLMs).
We perform a large-scale evaluation of MIAs over a suite of language models (LMs) trained on the Pile, ranging from 160M to 12B parameters. We find that MIAs barely outperform random guessing for most settings across varying LLM sizes and domains. Our further analyses reveal that this poor performance can be attributed to (1) the combination of a large dataset and few training iterations, and (2) an inherently fuzzy boundary between members and non-members.
We identify specific settings where LLMs have been shown to be vulnerable to membership inference and show that the apparent success in such settings can be attributed to a distribution shift, such as when members and non-members are drawn from the seemingly identical domain but with different temporal ranges.
For more, see https://iamgroot42.github.io/mimir.github.io/.
Post by Anshuman Suri and Fnu Suya
Much research has studied black-box attacks on image classifiers, where adversaries generate adversarial examples against unknown target models without having access to their internal information. Our analysis of over 164 attacks (published in 102 major security, machine learning and security conferences) shows how these works make different assumptions about the adversary’s knowledge.
The current literature lacks cohesive organization centered around the threat model. Our SoK paper (to appear at IEEE SaTML 2024) introduces a taxonomy for systematizing these attacks and demonstrates the importance of careful evaluations that consider adversary resources and threat models.
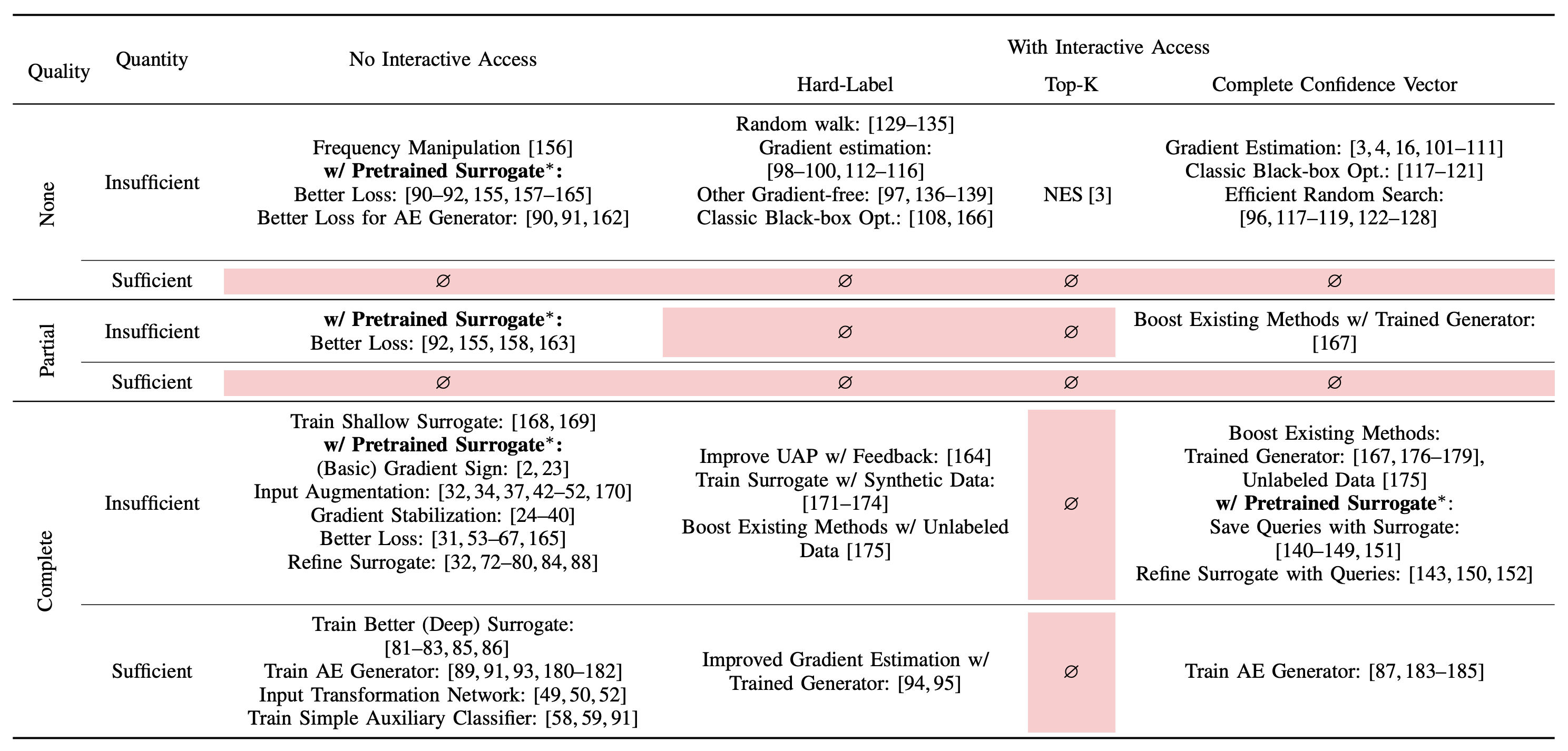
We propose a new attack taxonomy organized around the threat model assumptions of an attack, using four separate dimensions to categorize assumptions made by each attack.
Query Access: access to the target model. Under no interactive access, there is no opportunity to query the target model interactively (e.g., transfer attacks). With interactive access, the adversary can interactively query the target model and adjust subsequent queries by leveraging its history of queries (e.g., query-based attacks).
API Feedback: how much information the target model’s API returns. We categorize APIs into hard-label (only label returned by API), top-K (confidence scores for top-k predictions), or complete confidence vector (all confidence scores returned).
Quality of Initial Auxiliary Data: overlap between the auxiliary data available to the attacker and the training data of the target model. We capture overlap via distributional similarity in either feature space (same/similar samples used) or the label space. No overlap is closest to real-world APIs, where knowledge about the target model’s training data is obfuscated and often proprietary. Partial overlap captures scenarios where the training data of the target model includes some publicly available datasets. Complete overlap occurs where auxiliary data is identical (same dataset or same underlying distribution) to the target model’s training data.
Quantity of Auxiliary Data: does that adversary have enough data to train well-performing surrogate models, categorized as insufficient and sufficient.
Our taxonomy, shown below in the table, highlights technical challenges in underexplored areas, especially where ample data is available but with limited overlap with the target model’s data distribution. This scenario is highly relevant in practice. Additionally, we found that only one attack (NES) explicitly optimizes for top-k prediction scores, a common scenario in API attacks. These gaps suggest both a knowledge and a technical gap, with substantial room for improving attacks in these settings.
Our new top-k adaptation (figure below) demonstrates a significant improvement in performance over the existing baseline in the top-k setting, yet still fails to outperform more restrictive hard-label attacks in some settings, highlighting the need for further investigation.
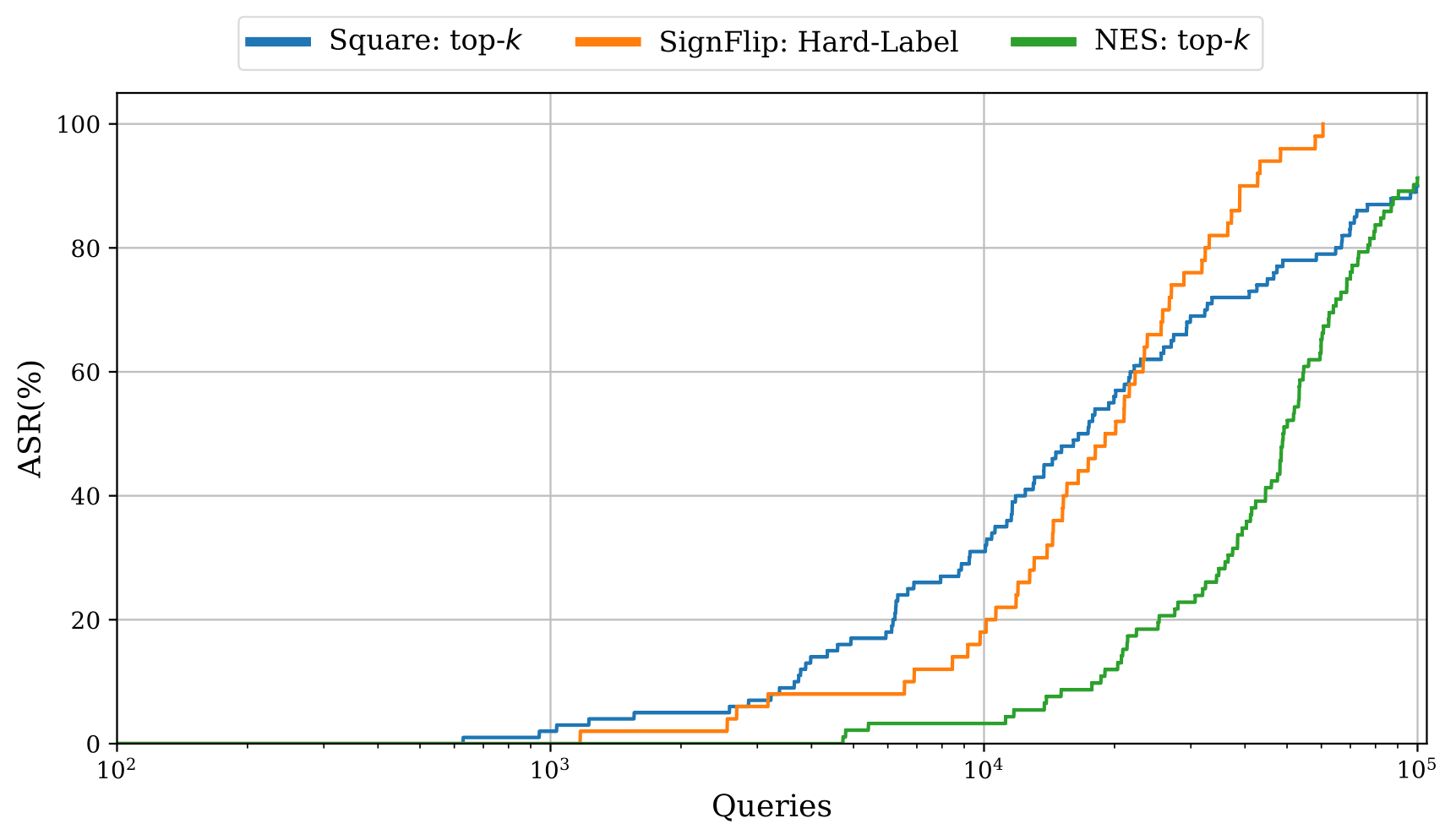
Comparison of top-k attacks. Square: top-k is our proposed adaption of the Square Attack for the top-k setting. NES: top-k is the current state-of-the-art attack. SignFlip is a more restrictive hard-label attack.
See the full paper for details on how the attacks were adapted.
Our study revealed that current evaluations often fail to align with what adversaries actually care about. We advocate for time-based comparisons of attacks, emphasizing their practical effectiveness within given constraints. This approach reveals that some attacks achieve higher success rates when normalized for time.
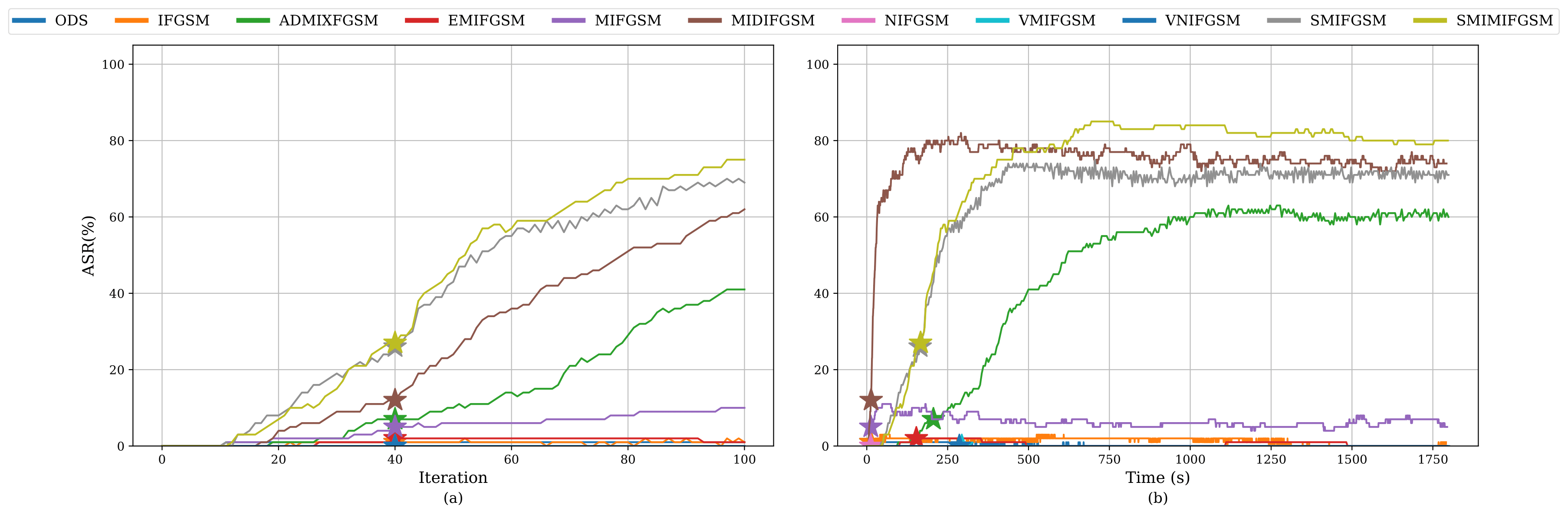
The paper underscores many unexplored settings in black-box adversarial attacks, particularly emphasizing the significance of meticulous evaluation and experimentation. A critical insight is the existence of many realistic threat models that haven’t been investigated, suggesting both a knowledge and a technical gap in current research. Considering the rapid evolution and increasing complexity of attack strategies, carefuly evaluation and consideration of the attack setting becomes even more pertinent. These findings indicate a need for more comprehensive and nuanced approaches to understanding and mitigating black-box attacks in real-world scenarios.
Fnu Suya*, Anshuman Suri*, Tingwei Zhang, Jingtao Hong, Yuan Tian, David Evans. SoK: Pitfalls in Evaluating Black-Box Attacks. In IEEE Conference on Secure and Trustworthy Machine Learning (SaTML). Toronto, 9–11 April 2024. [arXiv]
* Equal contribution
Code: https://github.com/iamgroot42/blackboxsok
Post by Fnu Suya
Data poisoning attacks are recognized as a top concern in the industry [1]. We focus on conventional indiscriminate data poisoning attacks, where an adversary injects a few crafted examples into the training data with the goal of increasing the test error of the induced model. Despite recent advances, indiscriminate poisoning attacks on large neural networks remain challenging [2]. In this work (to be presented at NeurIPS 2023), we revisit the vulnerabilities of more extensively studied linear models under indiscriminate poisoning attacks.
We observed significant variations in the vulnerabilities of different datasets to poisoning attacks. Interestingly, certain datasets are robust against the best known attacks, even in the absence of any defensive measures.
The figure below illustrates the error rates (both before and after poisoning) of various datasets when assessed using the current best attacks with a 3% poisoning ratio under linear SVM model.
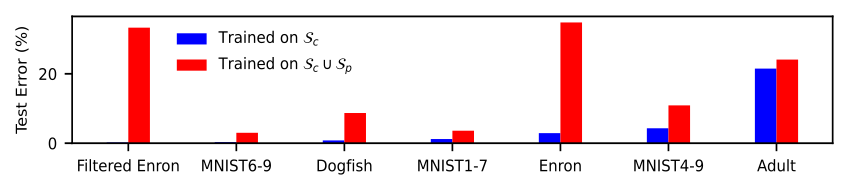
Here, $\mathcal{S}_c$ represents the original training set (before poisoning), and $\mathcal{S}_c \cup \mathcal{S}_p$ represents the combination of the original clean training set and the poisoning set generated by the current best attacks (the poisoned model). Different datasets exhibit widely varying vulnerability. For instance, datasets like MNIST 1-7 (with an error increase of <3% at a 3% poisoning ratio) display resilience to current best attacks even without any defensive mechanisms. This leads to an important question: Are datasets like MNIST 1-7 inherently robust to attacks, or are they merely resilient to current attack methods?
To address this question, we conducted a series of theoretical analyses. Our findings indicate that ditributions, which are characterized by high class-wise separability (Sep) and low in-class variance (SD), as well as smaller sizes for the set containing all poisoning points (Size), inherently exhibit resistance to poisoning attacks.
Returning to the benchmark datasets, we observed a strong correlation between the identified metrics and the empirically observed vulnerabilities to current best attacks. This reaffirms our theoretical findings. Notably, we employed the ratios Sep/SD and Sep/Size for convenient comparison between datasets, as depicted in the results below:
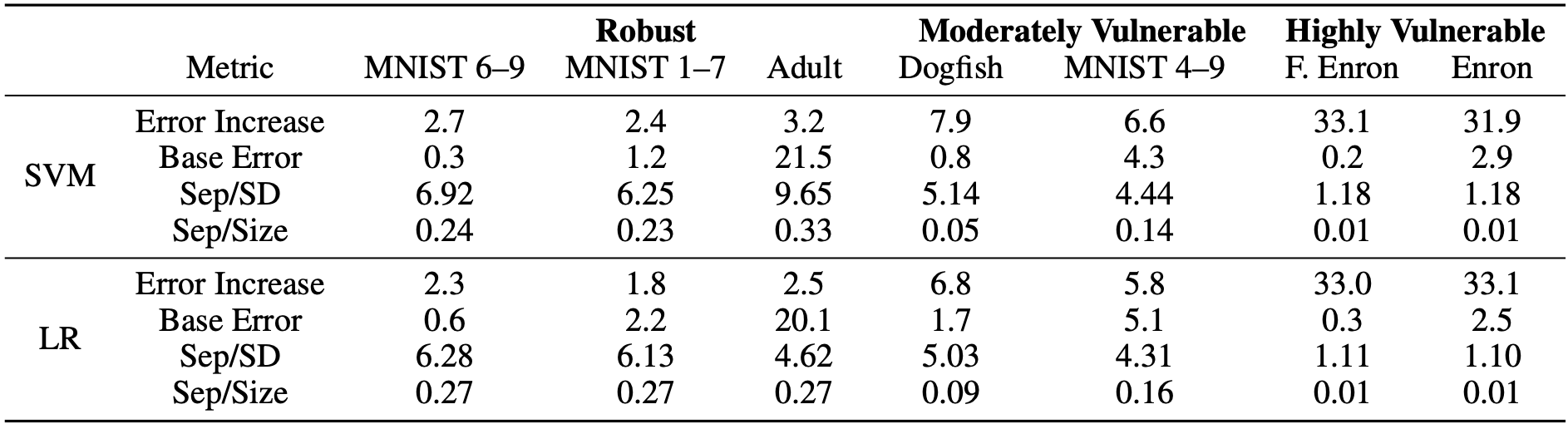
Datasets that are resistant to current attacks, like MNIST 1-7, exhibit larger Sep/SD and Sep/Size ratios. This suggests well-separated distributions with low variance and limited impact from poisoning points. Conversely, more vulnerable datasets, such as the spam email dataset Enron, display the opposite characteristics.
While explaining the variations in vulnerabilities across datasets is valuable, our overriding goal is to improve robustness as much as possible. Our primary finding suggests that dataset robustness against poisoning attacks can be enhanced by leveraging favorable distributional properties.
In preliminary experiments, we demonstrate that employing improved feature extractors, such as deep models trained for an extended number of epochs, can achieve this objective.
We trained various feature extractors on the complete CIFAR-10 dataset and fine-tuned them on data labeled “Truck” and “Ship” for a downstream binary classification task. We utilized a deeper model, ResNet-18, trained for X epochs and denoted these models as R-X. Additionally, we included a straightforward CNN model trained until full convergence (LeNet). This approach allowed us to obtain a diverse set of pretrained models representing different potential feature representations for the downstream training data.
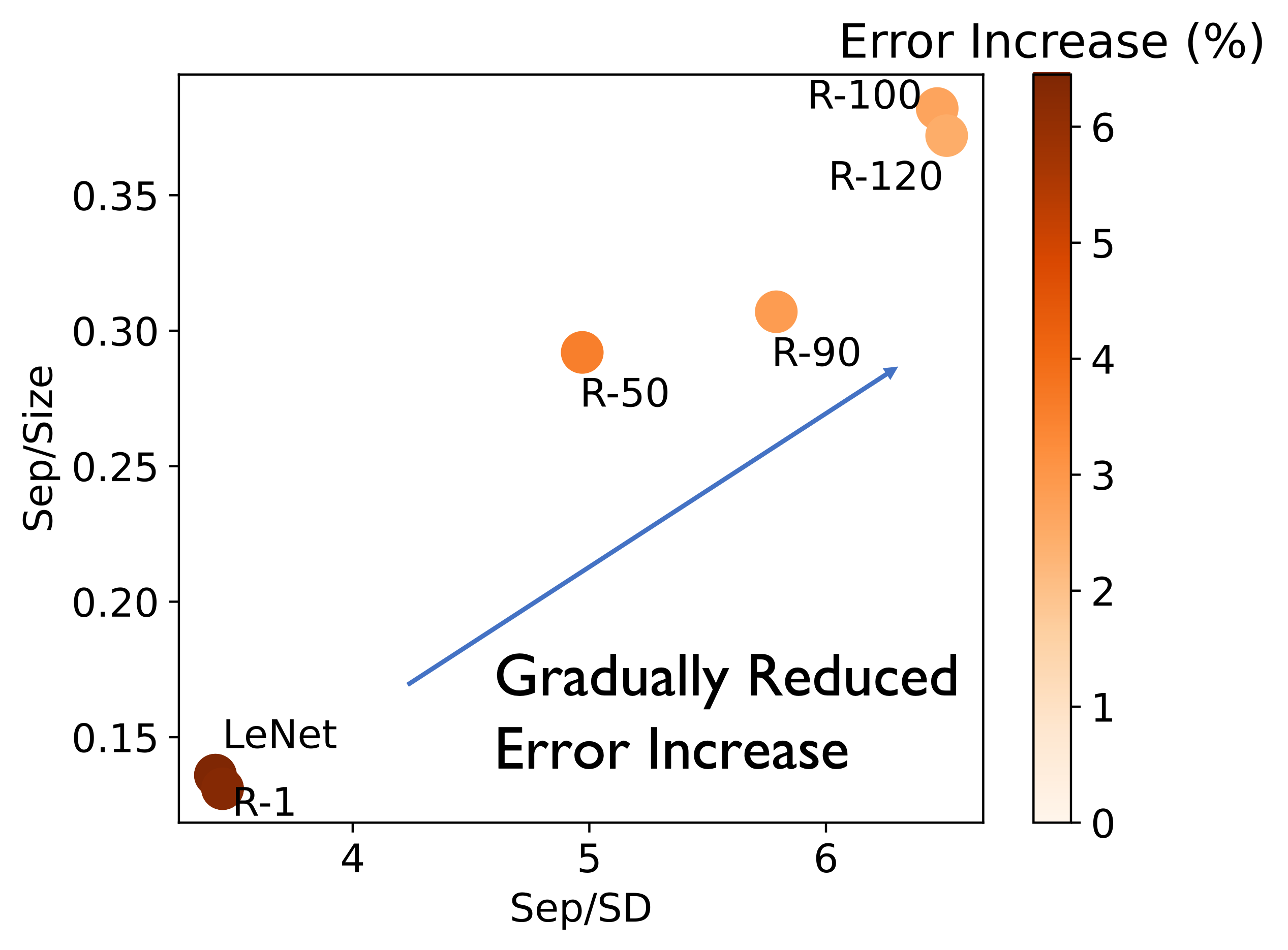
The figure above shows that as we utilize the ResNet model and train it for a sufficient number of epochs, the quality of the feature representation improves, subsequently enhancing the robustness of downstream models against poisoning attacks. These preliminary findings highlight the exciting potential for future research aimed at leveraging enhanced features to bolster resilience against poisoning attacks. This serves as a strong motivation for further in-depth exploration in this direction.
Fnu Suya, Xiao Zhang, Yuan Tian, David Evans. What Distributions are Robust to Indiscriminate Poisoning Attacks for Linear Learners?. In Neural Information Processing Systems (NeurIPS). New Orleans, 10–17 December 2023. [arXiv]